In mathematics, a system of linear equations is a collection of two or more linear equations with the same set of variables in all the equations.
In other words, we can say a system of linear equations is nothing but two or more equations that are being solved simultaneously.
Mostly, the system of equations can be used by the business people to predict their future events. They will model a real world situation in to system of equations to find the solution and manage their business. We can make an accurate prediction by using system of equations.
The solution of the system of equations is an ordered pair that satisfies each equation in the system.
Consider the two equations,
x + y = 2
x - y = 2
It forms a system of equations in two variables. The solution of this system is the ordered pair (x, y).
Consider the equations given below.
-3a + 2b - 6c = 6
5a + 7b - 5c = 6
a + 4b - 2c = 8
It forms a system of equations in three variables. The solution of this system is the ordered pair (a, b, c).
The solution of a system of linear equations can be of three types. They are:-
(i) One solution (ii) Infinite solution and (iii) No solution
If the graph of the equations intersects each other at a point, then ordered pair corresponding to the point of intersection will be the solution to that system. In this case, the system will have exactly one solution.
If a system has exactly one solution, then the equations are said to be independent.
If the graph of the equations coincides, then all the points on the line will be the solution to that system. In this case, the system will have infinite number of solutions.
If the system has infinite number of solutions, then the equations are said to be dependent.
If the graphs of the equations are parallel, then the system of equations will have no solution. Because parallel lines never intersect each other.
If the system has at least one solution (one solution or infinitely many solutions), then it is said to be consistent system.
If the system has no solution, then it is said to be inconsistent system.
The following figure will give clear picture of what we have learnt above.

Examples:
Discuss the number of solutions and type of the system of equations given in the graphs.
Discuss the number of solutions and type of the system of equations given in the graphs.
(i)
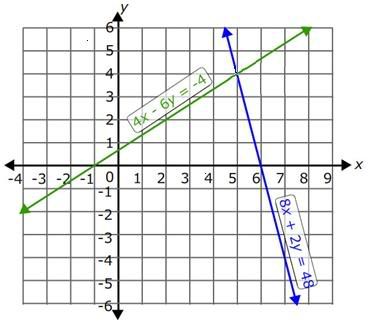
Solution:
Step 1:
The system of equations is
4x - 6y = -4
8x + 2y = 48
Step 2:
From the graph, it is clear that the two lines 4x - 6y = -4 and 8x + 2y = 48 intersect at exactly one point.
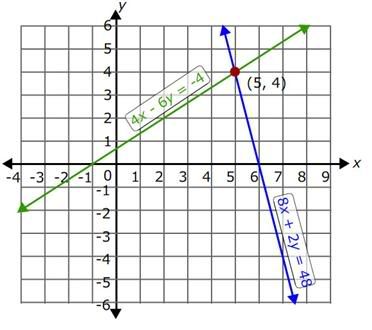
The point of intersection is (5, 4).
Step 3:
So, the system of equation has only one solution and hence it is consistent and independent.
(ii)
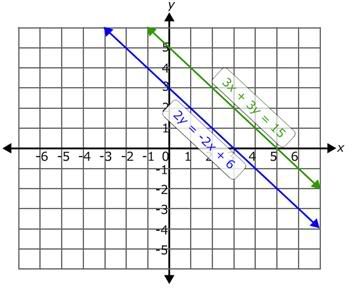
Solution:
Step 1:
The system of equations is
3x + 3y = 15
2y = -2x + 6

Step 2:
From the graph, it is clear that the two lines are parallel. Parallel lines never intersect.
Step 3:
So, there is no solution for this system of equations and the system is inconsistent.
(iii)

Step 1:
From the graph, it is clear that the two equations y = 3x + 2 and 6x - 2y + 4 = 0 coincide with each other.
Step 2:
All the points on the line are the solutions to both the equations. So, the system of equations has infinite number of solutions.
Step 3:
So, the system of equations is consistent and the equations are dependent.
Practice Questions:
Check the consistency of given system of equations. Are they dependent or independent?
a) 2x + 3y = 4; x – 5y = -11
b) 2x + 11y = 6; 2x + 11y = 7
c) 4x + 2y = 4; 6x + 3y = 6
d) x – 4y + 1 = 0; 4y – x = 1
e) 3x – y = -2; 4x – 9y = 5
You may also interested in this: