LCM: Least Common Multiple Worksheets

This tutorial explains how to find the least common multiple (some people say lowest common multiple) of any two or three given numbers with detailed example. LCM worksheets provided at the end of tutorial to practice.

LCM for any two numbers:

Least common multiple (LCM) for any given numbers is a lowest number which is divisible by all the numbers taken into account. Not clear??? Look at the following example.

Take any two numbers say 3 and 5. Now list the numbers that are divisible by both 3 and 5. We have 15, 30, 45, 60 and so on. Among those numbers which is smallest? Yes, you are right, it is 15. So, we can say that 15 is the lowest common multiple of 3 and 5. It is easy to find LCM for smaller numbers. Let us see how to find LCM for bigger numbers. Here is an example.

Find the LCM of 24 and 36:

It is really hard for anyone to find the number which is divisible by both 24 and 36. We are going to use the following trick to make it easy.

Use prime factor tree method to split numbers into product of primes.

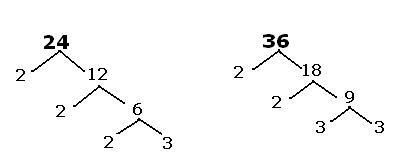
Taking only the primes, we can write 24 and 36 as below.

24 = 2 * 2 * 2 * 3

36 = 2 * 2 * 3 * 3

Take common primes once and then take uncommon primes as below:

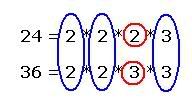
LCM = 2 * 2 * 3 * 2 * 3 = 72

72 is the least number which is divisible by both 24 and 36. Therefore 72 is the Least Common Multiple of 24 and 36.

LCM worksheets: Level 1

Find the least common multiple for the following pair of numbers.

a) 5, 7

b) 8, 9

c) 12, 15

d) 36, 48

e) 72, 96

LCM for any three numbers:

Procedure for finding least common multiple of any three numbers is not any more different that explained for two numbers. Anyway, here is an example for clear understanding.

Find the LCM of 12, 18 and 24:

Prime factorize 12, 18 and 24 using prime factor tree method.

What is our next step? Not sure? Refer previous example. Yes, you are right. We have to take common primes for all three numbers, then take common primes for any two numbers and then finally take all primes which is not yet considered.

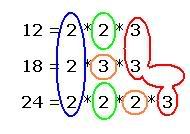
Circled with blue and red repeats in all three numbers. So, take it just once. We have 2 * 3.

Circled with green repeats in two places. Taking that once along with previous common factors, we have 2 * 3 * 2.

Look at the orange circle which never repeats in any places after picking all common primes.

Choosing them, we have 2 * 3 * 2 * 3 * 2.

Finally, we can say, LCM of 12, 18 and 24 = 2 * 3 * 2 * 3 * 2 = 72.

LCM worksheets: Level 2

What is the least common multiple for the given numbers?

a) 5, 7, 8

b) 8, 16, 32

c) 4, 12, 16

d) 24, 36, 42

e) 48, 56, 72

Few easy ways to find LCM:

1) If any two distinct numbers are prime, then LCM is product of those numbers.

For example, let’s take two prime numbers 5 and 7. LCM of 5 and 7 = 5 * 7 = 35

It works with any number of unique prime numbers.

Can you try the LCM of 5, 7 and 11?

LCM worksheets: Type 1

Find the lowest common multiple of the following.

a) 2, 3

b) 2, 3, 5

c) 7, 11

d) 11, 13

e) 3, 7

2) Are you familiar with Co-primes? Here is an example. Is 4 a prime? No. Is 9 a prime? No.

But 4 and 9 are co-prime. Have any guess why they are co-prime? I think you got the point. There are no common factors for 4 and 9. So, 4 and 9 are co-prime. LCM of co-prime numbers is just a product of those numbers. Do you understand this? What is the least common multiple for 4 and 9? Yes, you are right. It is just a product of 4 and 9. LCM of 4 and 9 = 4 * 9 = 36.

What is the LCM of 4, 9 and 25? Try it yourself.

What is the LCM of 3 and 4? Here 3 is prime, 4 is composite but both 3 and 4 are co-prime as it doesn’t contain common factors. So, LCM of 3 and 4 = 3 * 4 = 12

LCM worksheets: Type 2

Find the least common multiple for the given numbers:

a) 2, 9

b) 5, 6

c) 7, 8

d) 8, 11

e) 6, 11, 13

3) Now let’s take a number 4 and 8. What you can say about these numbers? 4 divides 8, isn’t it?

Therefore, LCM of 4 and 8 is just 8 itself. What is the LCM of 8 and 16? Yes, you are right. It is 16.

LCM worksheets: Type 3

Find the least common multiple of the following:

a) 5, 25

b) 2, 4, 8

c) 3, 9, 18

d) 6, 12

e) 14, 42

You may also interested in this:

>> Percent Word Problems

>> Ratio Word Problems

>> Area and Perimeter: Square and Rectangle

>> Age Word Problems

>> Equations in single variable: Quadrilaterals

>> Equations in single variable: Algebra

Fraction Word Problems

Fraction word problems for addition and subtraction is given here. This fraction word problems worksheet contains both proper and improper fractions. Student needs to be be really careful in understanding the real world situation of fraction word problems, needs to be cautious where to apply addition and subtraction.

Printable questions and answers for fraction word problems is given below. Student can download this fraction worksheet for free.

1)Stewart won 50 ¹/₅ dollars and Edward won 30 ²/₅ dollars in a race. What was the total cash price of the race?

Solution:

To find total amount, add 50 ¹/₅ and 30 ²/₅.

Here the denominators are equal.

50 ¹/₅ + 30 ²/₅ = 80 ³/₅.

Total cash prize = 80 ³/₅ dollars.

2) Mr. Mark’s family went for a trip. To make the journey interesting, they travelled first 53 ¹/₄ km by car and the remaining 10 ²/₃ km by horse ride. What was the total distance of the trip?

Solution:

To find the total distance, add 53 ¹/₄ and 10 ²/₃.

Let us convert the given mixed fractions into improper fractions.

53 ¹/₄= ²¹³/₄ and 10 ²/₃ = ³²/₃.

Here the denominators are unequal.

To make the denominators equal, we have to find the L.C.M of 3 and 4.

Multiples of 3= 3, 6, 9, 12 ….

Multiples of 4= 4, 8, 12, 16 ….

L.C.M= 12

To find common denominator, multiply both numerator and denominator of ²¹³/₄ by 3 and ³²/₃ by 4.

²¹³/₄ = ⁶³⁹/₁₂ ; ³²/₃ = ¹²⁸/₁₂

Now, ⁶³⁹/₁₂+ ¹²⁸/₁₂ = ⁷⁶⁷/₁₂ km = 63 ¹¹/₁₂ km

Total distance and covered = 63 ¹¹/₁₂ km.

3) Mr. White and Co. has total profit of ⁶/₇ of million dollars. The spinning department gave a profit of ¹/₂ of million dollars and weaving department gave a profit of ¹/₄ of million dollars. Find the fraction of profit from other departments.

Solution:

Total profit =⁶/₇

Profit from spinning and weaving departments=¹/₂ +¹/₄

Profit from other departments =⁶/₇-(¹/₂+¹/₄)

Here to make the denominators equal we have to find the L.C.M of 7, 2 and 4.

Multiples of 7= 7, 14, 21, 28 ….

Multiples of 2= 2, 4, 6, 8, 12, …, 26, 28 …

Multiples of 4= 4, 8, 12, 16, 20, 24, 28 …

L.C.M= 28.

⁶/₇= ^6*4/_7*4 = ²⁴/₂₈ (To make the denominator 28, multiply and divide by 4).

¹/₂= ^1*14/_2*14 =¹⁴/₂₈ (To make the denominator 28, multiply and divide by 14).

¹/₄=^1*7/_4*7 =⁷/₂₈ (To make the denominator 28, multiply and divide by 7).

Profit from other departments = ²⁴/₂₈-(¹⁴/₂₈+⁷/₂₈)

= ²⁴/₂₈ - ²¹/₂₈

= ³/₂₈

Therefore profit from other departments= ³/₂₈ of million dollars.

-----------------------------------------------------------------------------------

Fraction Word Problems Worksheet:

i) Three friends Christ, Marx and Davey participated in gun shooting events. Each of them was given 10 chances. They hit the targets 3 times, 2 times and 4 times respectively out of 10 chances each. Find the total targets hit by them in fraction.

ii) An side of an equilateral triangle is ³/₁₁ feet. Find the perimeter of a triangle.

iii) The length and width of a rectangle is ³/₂ cm and ¹/₂ cm respectively. Find the perimeter of a rectangle.

iv) Sam celebrates his birthday with two small cakes. 7 people attended the birthday party. What fraction of cake each one will receive excluding Sam?

v) Nick and Robert have worked together and completed ³/₄ of work in a day. Robert has done ²/₅ of work. Find the work done by Nick.

vi) Mr. Briar, principal of Edward Public School, collects funds for School development. ²/₃ of funds are collected from school students and ¹/₆ of funds are collected from school development charity and the rest are collected from Public. What fraction of funds collected from public?

vii) Anne has 1 pizza, Eris ton has 1 ³/₄ of pizza and Julie has ¹/₇ of pizza. Find the total number of pizzas.

viii) To make a milk shake, 2 gallons of milk, ¹/₇ of gallons of essence and ³/₄ of gallons of fruit juice were required. Find the total gallons of milk shake made out of it.

ix) Harris has to travel 2 ²/₃ of a mile. He walked 1 ¹/₃ of the distance and the remaining by car. Find the distance covered by car.

x) Kate and Tony took part in running race. They covered a distance of ⁵/₈ yards and ⁸/₉ yards respectively. Find the distance between these athletes.
Download:
Questions:
   Answers:  

Related Articles:

>> 1st Grade Math Worksheet

>> 2nd Grade Math Worksheet

>> 3rd Grade Math Worksheet

>> 4th Grade Math Worksheet

>> 5th Grade Math Worksheet

>> Addition and Subtraction Word Problems

Ratio - Simple word problems worksheet

1) Find the ratio of 36 yards to 48 yards.

Solution:
36 yards : 48 yards
= 36 : 48
Dividing both numbers by 2 (to avoid more steps we can also divide it by GCD)
= 18 : 24
Dividing both numbers by 2
= 9 : 12
Dividing both numbers by 3
= 3 : 4
This is the simplest form which is not reducible further.
36 yards : 48 yards = 3 : 4

2) Find the ratio of 65 days to 50 days.

Solution:
65 days : 50 days
65 : 50
Dividing both numbers by 5
13 : 10
This is the simplest form.
65 days : 50 days = 13 : 10

------------------------------------------------------------------------------------

Practice questions:

Find the ratio of
i) 200 m to 600 m
ii) 350 bags to 500 bags
iii) 25 feet to 125 feet
iv) 150 pencils to 225 pencils
v) 69 km to 96 km
vi) 22 yards to 77 yards
vii) 36 hours to 60 hours
viii) $64 to $48
ix) 121 inches to 99 inches
x) 138 cookies to 186 cookies

-----------------------------------------------------------------------------------

3) Find the ratio of 36 hours to 2 days.

Solution:
1 day = 24 hours
2 days = 2 * 24 = 48 hours
36 hours : 2 days
= 36 hours : 48 hours
= 36 : 48
Dividing by 6 ( Use 2 to divide if not familiar with 6 )
= 6 : 8
Dividing by 2
= 3 : 4

4) Find the ratio of $2.50 to 75 cents.

Solution:1 dollar = 100 cents
2.50 dollar = 2.50 * 100 = 250 cents
$2.50 to 75 cents
= 250 cents : 75 cents
= 250 : 75
Dividing by 25
= 10 : 3

-----------------------------------------------------------------------------------------------
Practice questions:

Find the ratio of
i) 12 inches to 3 feet
ii) 12 feet to 7 yards
iii) $1.25 to half a dollar
iv) 8 quarters to 5 nickels
v) 36 pints to 4 gallons
vi) 20 ounces to 1.5 pounds
vii) 45 cm to 2 meter
viii) 3 hours 20 minutes to 2 hours 10 minutes
ix) 1250 feet to 1 mile
x) 12 cm to 1.2 cm

-----------------------------------------------------------------------------------------------
5) There are 250 students in a certain school. If the number of boys in a school are 120. Find the ratio between
i) number of girls to number of boys
ii) number of boys to total number of students
iii) number of students to number of girls

Solution:
Number of students = 250
Number of boys = 120
Number of girls = Total number of students – Total number of boys
= 250 – 120
= 130

i) Number of girls to number of boys
= number of girls : number of boys
= 130 : 120
Dividing each term by 10
= 13 : 12
So, ratio between girls to the boys is 13 : 12

ii) Number of boys to total number of students
= number of boys : number of students
= 120 : 250
Dividing each term by 10
= 12 : 25
So, ratio between boys to the students is 12 : 25

iii) Number of students to number of girls
= number of students : number of girls
= 250 : 130
Dividing each term by 10
= 25 : 13
So, ratio between students to the girls is 25 : 13

6) Mr. Mac has 12 white balls, 15 black balls and 18 green balls. Find the ratio of
i) Black balls to white balls
ii) White balls to total number of balls
iii) Black balls to white balls to green balls

Solution:
Number of white balls = 12
Number of black balls = 15
Number of green balls = 18
Total number of balls = 12 + 15 + 18
= 45

i) Black balls to white balls
= black balls : white balls
= 15 : 12
Dividing each term by 3
= 5 : 4
So, the ratio of black balls to white balls is 5 : 4

ii) White balls to total number of balls
= white balls : total number of balls
= 12 : 45
Dividing each term by 3
= 4 : 15
So, the ratio of white balls to total number of balls is 4 : 15

iii) Black balls to white balls to green balls
= black balls : white balls : green balls
= 15 : 12 : 18
Dividing each term by 3
= 5 : 4 : 6
So, the ratio of black balls to white balls to green balls is 5 : 4 : 6

---------------------------------------------------------------------------------------

Practice questions:

i) Mrs. Alice earns $ 1200 per month. She spends $ 800 and saves the rest. Find the ratio of her salary to savings ?
ii) Anne scored 40 points out of 50. Find the ratio between the number of points scored to total number of points.
iii) In grade six, 36 students were passed. Total students in a class are 48. Find the ratio of passed students to the failed students.

Venn Diagram - Word Problems

1) Stephen asked 100 coffee drinkers whether they like cream or sugar in their coffee. According to the Venn diagram below, how many like

a) Cream?

b) Sugar?

c) Sugar but not cream?

d) Cream but not sugar?

e) Cream and sugar?

f) Cream or sugar?

Solution:

a) 16 + 20 = 36

b) 20 + 35 = 55

c) 35

d) 16

e) 20

f) 16 + 20 + 35 = 71

Practice Questions:

2) Eon asked 60 students whether they listen to two popular radio stations, WROK and WRAP. He found that 23 listen to WROK, 18 listen to WRAP, and 8 listen to both. How many students in Robert's survey listen to

a) WROK but not WRAP

b) WRAP but not WROK

c) neither WROK nor WRAP

3)Oshkosh did a study of the colors used in African national flags. He found that 38 flags have red, 20 have blue, 13 have both red and blue, and 8 have neither red nor blue. How many flags

a. have red but not blue?

b. have blue but not red?

c. were inclulded in the study?

4) Kroner asked 100 adults whether they had studied French, Spanish or Japanese in school. According to the Venn diagram below, how many had studied

a. Spanish?

b. Spanish but not French?

c. Japanese but not French?

d. French and Spanish?

e. French or Spanish?

f. French and Spanish but not Japanese?

5. Coach Krutch offered to buy hot dogs for players on his team. Of the 44 players, 28 wanted ketchup, 20 wanted mustard, 14 wanted relish, 10 wanted ketchup and mustard, 11 wanted ketchup and relish, 8 wanted mustard and relish and 6 wanted all three condiments. How many players wanted

a. Ketchup only?

b. Mustard but not relish?

c. Relish but not mustard?

d. Ketchup and mustard but not relish?

e. Relish and mustard but not ketchup?

f. None of the three condiments?

Area and Perimeter - Square and Rectangle

1) Find the perimeter and area of a rectangle with width 6 feet and length 14 feet.

Solution:

Length = 14 ft

Width = 6 ft

Perimeter of a rectangle = 2(l + w) = 2(14+6) = 2(20) = 40 ft.

Area of a rectangle = length * width = 14 * 6 = 84 square feet.


2) Find the area and perimeter of a rectangle with length 42 and width 12.

Solution:

Length = 42

Width = 12

Perimeter of a rectangle = 2(l + w) = 2(42+12) = 2(54) = 108 units.

Area of a rectangle = length * width = 42 * 12 = 504 square units.


--------------------------------------------------------------------------------------------------------


Practice questions:


i) Find the perimeter and area of a rectangle with length 12 yards and width 6 yards.

ii) Find the perimeter and area of a rectangle whose length is 5 yards and width is 6 feet. ( Hint: 3 feet = 1 yard )

iii) Find the area and perimeter of a given rectangle ( see figure1)




iv) Length and width of a rectangle is 11 inches and 5 inches respectively. Find its area and perimeter.

v) In a rectangle, length = 12.5 cm and width = 7.5 cm. Find its area and perimeter.

vi) Dimensions of a rectangle are given in figure 2. Find the area and perimeter of a rectangle.



vii) If the length and width of a rectangle is 39 inches and 2 feet respectively, find its area and perimeter.(Hint: 1 foot = 12 inches)

viii) Find the area and perimeter for a given figure 3.



ix) Area of a rectangle is 25 sq. cm. What is the total area of 5 such rectangles?

x) The length and width of a rectangle is 3 inches and 5 inches respectively. Find the perimeter of a rectangle formed by joining the width of such 3 rectangles.


------------------------------------------------------------------------------------------------


3) Find the perimeter and area of a square with side 11 meters.

Solution:

Side =11 m

Perimeter of a square = 4 * side = 4 * 11 = 44 m

Area of a square = side * side = 9 * 9 = 81 sq. m


4) Find the area and perimeter of a square with side 5.5 cm.

Solution:

Side =5.5 cm

Perimeter of a square = 4 * side = 4 * 5.5 = 22 cm

Area of a square = side * side = 5.5 * 5.5 = 30.25 sq. cm


-------------------------------------------------------------------------------------------------


Practice questions:

i) Find the perimeter and area of a square with side 12 feet.

ii) Find the area and perimeter of a given square ( see figure 4)





iii) Find the perimeter and area of a square with side 8.2 cm.

iv) If the side of a square measures 4 yards, find its perimeter and area.

v) Find the area and perimeter of a given figure 5.


vi) Find the area of a square of length 12 yards. Also find its perimeter.

vii) Area of a square is 2 sq. ft. What is the area of a figure formed by 20 such squares?

viii) Length of a square is 8 cm. How many such squares can be arranged to form a rectangle of length 24 cm and width 16cm.

ix) Length and width of a rectangle is 4.5 inches and 2 inches respectively. If a square is perfectly attached to the width of the rectangle, what is the total area of the new rectangle formed?

x) A rectangle with length 10 yards and width 4 yards are cut into squares. What is the maximum possible area of a square?



For Percent word problems click here



Kindly post your valuable comments below

Percent - Simple Word Problems

1) Nova school students are good players of Soccer. They won 16 games out of 20 played. Find the percentage of games won by Nova school students.

Solution:
Total number of games = 20
Number of games won = 16
Fraction of games won = 16 out of 20 = 16/20
% of games won = 16/20­­­­­* 100 = 1600/­­20 = 80%
Percentage of games won by Nova school students = 80

2) In a play school, 12 balls are red, 14 balls are green, 16 balls are white and 8 balls are blue. Find the percentage of i) Blue balls and ii) White balls

Solution:
Total number of balls = 12 + 14 + 16 + 8 = 50
i) Number of Blue balls = 8
Fraction of Blue balls = 8 out of 50 = 8/50
% of Blue balls = 8/50* 100 = 800/50 = 16%
Percentage of Blue balls = 16%
ii) Number of White balls = 16
Fraction of White balls = 16 out of 50 = 16/50
% of White balls = 16/50* 100 = 1600/50= 32%
Percentage of White balls = 32%

-------------------------------------------------------------------------------------------------
Practice questions:

1) Shop keeper bought 250 apples. He sold 75 apples for $30, 23 apples for $8.05, 82 apples for $24.6 and remaining apples were spoiled.
i) What percent of apples were spoiled?
ii) What percent of apples were sold for $30?
iii) What percent of apples were sold for $82

2) In a lucky draw, Paul won $1250. He spent $250 on watch, $150 on clothes, $350 on car moderation and saved the rest.
i) What percent of money he saved?
ii) What percent of money he spent on watch?
iii) What percent of money he spent on car moderation?

3) In a certain town, poll is conducted; Party A and Party B were only two nominees. Party A won by 12500 votes. Party B had been voted by 125000 people. No wrong votes were registered.
i) Find the percentage of lead by Party A
ii) Find the percentage of votes received by Party A
iii) Find the percentage of votes received by Party B

-------------------------------------------------------------------------------------------------

3) Ronnie had 25 cookies and gave 36% of cookies to his friend Mark. Find the number of cookies Mark received.

Solution:
Number of cookies = 25
Percentage of cookies given = 36%
Convert percentage into decimals by dividing 36 by 100
36% = 0.36
Number of cookies received by Mark
= 36% of 25
= 0.36 * 25
= 9
Mark can receive 9 cookies.

4) In a garden, 20% of trees are Guava, 35% of trees are Orange and rests of the trees are Mango.
If there are 500 trees in total, find the number of Mango trees.

Solution:
Total number of trees = 500
Percentage of Guava trees = 20%
Percentage of Orange trees = 35%
Percentage of Mango trees = 100% - 20% - 35% = 45%
Convert percentage into decimals by dividing 45 by 100
45% = 0.45
Number of Mango trees
= 45% of 500
= 0.45 * 500
= 225
There are 225 Mango trees.
-------------------------------------------------------------------------------------------------

Practice questions:

1) An old rich man holds property worth $2 million. He gave 38% of his property to his grand children, 5% to educational trust, 30% to his children.
i) What is the worth of property his children can get?
ii) What is the worth of property educational trust can get?

2) A shop keeper ordered 1550 books of which 24% are story books, 44% are computer books and rest are related with other topics.
i) Find the number of story books.
ii) Find the number of computer books.
iii) Find the number of books related with other topics.

Kindly post your valuable comments