Best method to solve quadratic equations

 So far, we have studied the four methods to solve a quadratic equation. How do we select the best method to solve among these four methods?

The following table will guide us to choose the best method to solve.

Method	When to choose
Graphing	Use if we need only the appropriate solutions. However, we can use it always.
Factoring	Use if we could easily determine the factors or the constant term is zero.
Completing the Square	Use if the equation is of the form x2 + bx + c = 0 and b is even. However, we can use it always.
Quadratic Formula	We can use this method to any type of quadratic equation. In some cases, the other methods will be easy to solve.

Example:

The product of two consecutive positive odd integers is 99. Find those two numbers.

Solution:

Step 1:

Given that the product of two consecutive positive odd integers is 99.

We are asked to find the two consecutive positive odd integers.

Let the first integer be x.

Then the consecutive positive odd integer is x + 2.

Given that the product of x and x + 2 = 99

=> x(x + 2) = 99

=> x² + 2x - 99 = 0

So, we arrived at a quadratic equation x² + 2x - 99 = 0.

Step 2:

We can solve the quadratic equation by using factoring.

x² + 11x - 9x - 99 = 0

=> x(x + 11) - 9(x + 11) = 0

=> (x + 11)(x - 9) = 0

=> x + 11 = 0 or x - 9 = 0

=> x = -11 or x = 9

Step 3:

Since we are looking for a positive number, neglect -11.

So, x = 9.

If x = 9, then x + 2 = 9 + 2 = 11.

Step 4:

Hence, the two consecutive positive odd numbers are 9 and 11.

Related Articles:

>> Graphing method to solve quadratic equations

>> Quadratic formula method to solve quadratic equations

>> Perfect Square Method: Detailed Review

>> Solving Quadratic Equations: Perfect Square Method

>> Solving Quadratic Equations: Factoring Method

>> Solving Inequalities: Graphing Method

>> Solving Linear Equations: Graphing Method

>> Linear Equations: Word Problems

Graphing Method: Quadratic Equations

In this method, we are going to find the solution or roots of a quadratic equation graphically. The graph of a quadratic equation is always a parabola. The points where the graph of the parabola cuts the x-axis are called the roots of the corresponding quadratic equation.

To graph a quadratic equation, we should graph the related quadratic function. For example, if the quadratic equation is x² + 2x + 5 = 0, then the related quadratic function is f(x) = x² + 2x + 5.

Let us solve few problems on quadratic equations by graphing.

Example 1:

Solve x² + x - 6 = 0 by graphing.

Solution:

Step 1:

Given equation is x² + x - 6 = 0.

Here a = 1, b = 1, and c = -6.

Graph the related function f(x) = x² + x - 6.

The equation of the axis of symmetry is x = - ^b/_2a

x = - ^b/_2a = - ¹/₂₍₁₎  = - ¹/₂ = -0.5

=> x = -0.5 is the axis of symmetry of the equation.

Step 2:

When x = -0.5,

f(x) = f(-0.5) = (-0.5) ² + (-0.5) - 6 = 0

=> f(-0.5) = 0.25 - 0.5 - 6 = -6.25

So, the coordinates of the vertex are (-0.5, -6.25).

Step 3:

Now, make the table with all other points.

Put x = -4, -3, -2, 0, 1, 2, 3 and find f(x).

When x = -4,

f(x) = f(-4) = (-4)² + (-4) - 6 = 16 - 4 - 6 = 6

When x = -3,

f(x) = f(-3) = (-3)² + (-3) - 6 = 9 - 3 - 6 = 0

When x = -2,

f(x) = f(-2) = (-2)² + (-2) - 6 = 4 - 2 - 6 = -4

When x = -1,

f(x) = f(-1) = (-1)² + (-1) - 6 = 1 - 1 - 6 = -6

When x = 0,

f(x) = f(0) = (0)² + (0) - 6 = 0 + 0 - 6 = -6

When x = 1,

f(x) = f(1) = (1)² + (1) - 6 = 1 + 1 - 6 = -4

When x = 2,

f(x) = f(2) = (2)² + 2 - 6 = 4 + 2 - 6 = 0

When x = 3,

f(x) = f(3) = (3)² + 3 - 6 = 9 + 3 - 6 = 6

x	-4	-3	-2	-1	-0.5	0	1	2	3
f(x)	6	0	-4	-6	-6.25	-6	-4	0	6

Hence, the ordered pairs of the quadratic function are (-4, 6), (-3, 0), (-2, -4), (-1, -6), (-0.5, -6.25), (0, -6), (1, -4), (2, 0), and (3, 6).

Step 4:

Now, plot the ordered pairs in a coordinate plane and join the points.

The point where the related function f(x) = 0 is the solution to this quadratic equation. This occurs at the x-intercepts. The x-intercepts are the points where the graph touches the x-axis. So, the graph has -3 and 2 as x-intercepts.

So, the solutions are -3 and 2.

Step 5:

Check:

We can also check our solutions by factoring the given equation.

x² + x - 6 =0

=> x² + 3x - 2x - 6 = 0

=> x(x + 3) - 2(x + 3) = 0

=> (x + 3)(x - 2) = 0

Using the zero product property,

x + 3 = 0 or x - 2 = 0

x = -3 or x = 2

Step 6:

So, the solutions of the equation are -3 and 2.

Example 2:

Solve x² - 10x + 25 = 0 by graphing.

Solution:

Step 1:

Given equation is x² - 10x + 25 = 0.

Here a = 1, b = -10, and c = 25.

Graph the related function f(x) = x² - 10x + 25.

The equation of the axis of symmetry is x = - ^b/_2a

x = - ^b/_2a = - ¹⁰/₂₍₁₎ = - ^b/_2a = 5

=> x = 5 is the axis of symmetry of the given equation.

Step 2:

When x = 5,

f(x) = f(5) = (5)² - 10(5) + 25 = 25 - 50 + 25 = 0

=> f(x) = 0

So, the coordinates of the vertex are (5, 0).

Step 3:

Now, make the table with all other points.

Put x = 2, 3, 4, 6, 7, 8 and find f(x).

When x = 2,

f(x) = f(2) = (2)² - 10(2) + 25 = 4 - 20 + 25 = 9

When x = 3,

f(x) = f(3) = (3)² - 10(3) + 25 = 9 - 30 + 25 = 4

When x = 4,

f(x) = f(4) = (4)² - 10(4) + 25 = 16 - 40 + 25 = 1

When x = 6,

f(x) = f(6) = (6)² - 10(6) + 25 = 36 - 60 + 25 = 1

When x = 7,

f(x) = f(7) = (7)² - 10(7) + 25 = 49 - 70 + 25 = 4

When x = 8,

f(x) = f(8) = (8)² - 10(8) + 25 = 64 - 80 + 25 = 9

x	2	3	4	5	6	7	8
f(x)	9	4	1	0	1	4	9

So, the ordered pairs of the quadratic function are (2, 9), (3, 4), (4, 1), (5, 0), (6, 1), (7, 4), and (8, 9).

Step 4:

Now, plot the ordered pairs in a coordinate plane and join the points.

The resultant graph will be as shown.

The point where the related function f(x) = 0 is the solution to this quadratic equation. This occurs at the x-intercepts. The x-intercepts are the points where the graph touches the x-axis.

Notice that the vertex of the parabola is the x-intercept.

Hence, the solution is 5.

Step 5:

Check:

Let us check it by factoring.

Factor the equation x² - 10x + 25 = 0.

x² - 5x - 5x + 25 = 0

=> x(x - 5) - 5(x - 5) = 0

=> (x - 5)(x - 5) = 0

=> x - 5 = 0 or x - 5 = 0

=> x = 5 or x = 5

So, there are two roots but they are identical.

So, this quadratic equation has only one root called 5 as double root.

Step 6:

So, the solution is 5.

Example 3:

Solve x² + 2x + 5 = 0 by graphing.

Solution:

 Step 1:

Given equation is x² + 2x + 5 = 0.

Here, a = 1, b = 2, and c = 5.

Graph the related function f(x) = x² + 2x + 5.

The equation of the axis of symmetry is x = - ^b/_2a

x = - ^b/_2a= - ²/₂₍₁₎ = -1

=> x = -1 is the axis of symmetry of the given equation.

Step 2:

When x = -1,

f(x) = f(-1) = (-1)² + 2(-1) + 5 = 1 - 2 + 5 = 4

So, the coordinates of the vertex are (-1, 4).

Now, make the table with all other points.

Put x = -4, -3, -2, 0, 1, 2 and find f(x).

When x = -4,

f(x) = f(-4) = (-4)² + 2(-4) + 5 = 16 - 8 + 5 = 13

=> f(-4) = 13

When x = -3,

f(x) = f(-3) = (-3)² + 2(-3) + 5 = 9 - 6 + 5 = 8

=> f(-3) = 8

When x = -2,

f(x) = f(-2) = (-2)² + 2(-2) + 5 = 4 - 4 +5 = 5

=> f(-2) = 5

When x = 0,

f(x) = f(0) = (0)² + 2(0) + 5 = 5

=> f(0) = 5

When x = 1,

f(x) = f(1) = (1)² + 2(1) + 5 = 1 + 2 + 5 = 8

=> f(1) = 8

When x = 2,

f(x) = f(2) = (2)² + 2(2) + 5 = 13

=> f(2) = 13

x	-4	-3	-2	-1	0	1	2
f(x)	13	8	5	4	5	8	13

So, the ordered pairs of the quadratic function are (-4, 13), (-3, 8), (-2, 5), (-1, 4), (0, 5), (1, 8), and (2, 13).

Step 3:

Now, plot the ordered pairs in a coordinate plane and join the points.

The resultant graph will be as shown.

The point where the related function f(x) = 0 is the solution to this quadratic equation. This occurs at the x-intercepts. The x-intercepts are the points where the graph touches the x-axis. So, the graph has no x-intercept.

Step 4:

So, there are no real number solutions for the given quadratic equation.

Here is some practice questions: Quadratic equations

To check your result: Quadratic equation solver

Related Articles:

>> Quadratic formula method to solve quadratic equations

>> Perfect Square Method: Detailed Review

>> Solving Quadratic Equations: Perfect Square Method

>> Solving Quadratic Equations: Factoring Method

>> Solving Inequalities: Graphing Method

>> Solving Linear Equations: Graphing Method

>> Linear Equations: Word Problems

Graphing Method: Solving Linear Equations

System of linear equations can be solved in three different ways. They are

a)      Solving system of equations by graphing.

b)     Solving system of equations by substitution.

c)      Solving system of equations by elimination.

Solving systems of linear equations by Graphing:

It is a method of solving linear system of equations. In this method, we graph the given equations on the coordinate plane and look for the points of intersection. The point of intersection determines whether the system of linear equations has no solution, one solution, or infinitely many solutions.

Let us explain this method by few examples.

Example 1:

Solve the system of equations graphically.

x + y = 4

x - y = 2

Solution:

Step 1:

To solve a system of equations graphically, first graph the given two lines and then look for the point of intersection of those two lines. The point of intersection is the solution to the given system of equations.

Step 2:

Graph the linear equations on a coordinate plane by making a table of x and y values.

 To find the value of y, first we need to solve the equation for y.

Step 3:

Consider the first equation x + y = 4.

Subtract x from both sides of the equation.

x - x + y = 4 - x

y = -x + 4

Now, randomly assign some values for x and find the corresponding values for y and make a table.

If x = -2, then y = -(-2) + 4 = 2 + 4 = 6

If x = -1, then y = -(-1) + 4 = 1 + 4 = 5

If x = 0, then y = -(0) + 4 = 4

If x = 1, then y = -(1) + 4 = 3

If x = 2, then y = -(2) + 4 = 2

If x = 3, then y = -(3) + 4 = 1

If x = 4, then y = -(4) + 4 = 0

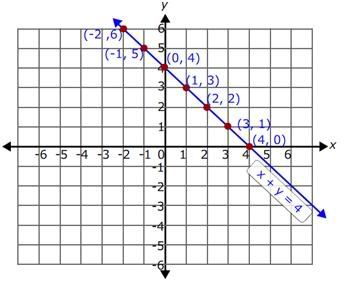
So, the table of values of the equation x + y = 4 is

x	-2	-1	0	1	2	3	4
y = -x + 4	6	5	4	3	2	1	0

So, the ordered pairs for the equation x + y = 4 are (-2, 6), (-1, 5), (0, 4), (1, 3), (2, 2), (3, 1), (4, 0).

Step 4:

Plot all the above ordered pairs on the coordinate plane and join all the points.

Step 5:

Consider the second equation x - y = 2.

Subtract x from both the sides of the equation.

x - x - y = 2 - x

Now, simplify it.

            -y = -x + 2

Multiply by (-1) on both the sides of the equation.

            y = x - 2

Now, randomly assign some values for x and find the corresponding values for y and make a table.

If x = -2, then y = -2 - 2 = -4

If x = -1, then y = -1 - 2 = -3

If x = 0, then y = 0 - 2 = -2

If x = 1, then y = 1 - 2 = -1

If x = 2, then y = 2 - 2 = 0

If x = 3, then y = 3 - 2 = 1

If x = 4, then y = 4 – 2 = 2

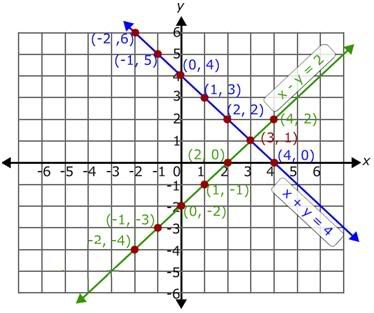
So, the table of values of the equation x - y = 2 is

x	-2	-1	0	1	2	3	4
y = x - 2	-4	-3	-2	-1	0	1	2

So, the ordered pairs for the equation x - y = 2 are (-2, -4), (-1, -3), (0, -2), (1, -1), (2, 0), (3, 1), (4, 0).

Step 6:

Plot all the above ordered pairs on the same coordinate plane and join all these points. 

The resulting graph is as shown.

Step 7:

The point of intersection of the two lines is (3, 1).

Step 8:

So, (3, 1) is the solution for the given system of equations.

Checking the solution:

We can also check the solution by replacing the value of x and y in the two equations.

Replace the value of x by 3 and y by 1 in the equation y = -x + 4.

1 = -3 + 4

1 = 1

So, (3, 1) satisfies the equation y = -x + 4. 

Replace the value of x by 3 and y by 1 in the equation y = x - 2.

1 = 3 - 2

1 = 1

So, (3, 1) also satisfies the equation y = x - 2.

Step 9:

So, (3, 1) is the solution for the given system of equations and the system of equations is consistent and the equations are independent.

Example 2:

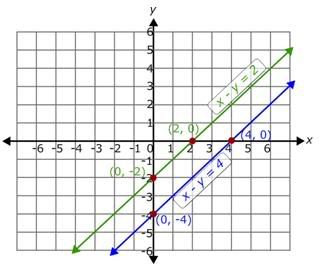
Solve the system of equations graphically.

x – y = 4

x – y = 2

Solution:

Step 1:

To solve a system of equations graphically, first graph the given two lines and then look for the point of intersection of those two lines. The point of intersection is the solution to the given system of equations.

Step 2:

Graph both the equations on the coordinate plane.

We can also graph the linear equations using the x and y-intercept.

Step 3:

Consider the first equation x - y = 4.

Replace x by 0 in the above equation, then we will get the y-intercept.

0 - y = 4

y = -4

For x = 0, the value of y is -4.

So, the ordered pair is (0, -4).

Now, replace y by 0 in the equation x - y = 4, then we will get the x-intercept.

x - 0 = 4

x = 4

For y = 0, the value of x is 4.

So, the ordered pair is (4, 0).

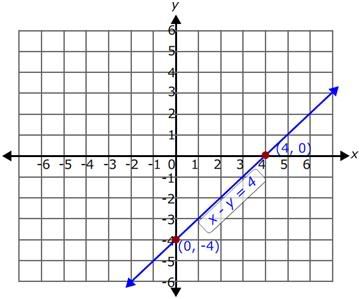
Thus, we get the two ordered pairs (0, -4) and (4, 0).

Step 4:

Now, plot these two ordered pairs on the coordinate plane and join them. 

Step 5:

Similarly, consider the second equation x - y = 2.

Replace x by 0 in the above equation, then we will get the y-intercept.

0 - y = 2

y = -2

For x = 0, the value of y is -2.

So, the ordered pair is (0, -2).

Replace y by 0 in the above equation, then we will get the x-intercept.

x - 0 = 2

x = 2

For y = 0, the value of x is 2.

So, the ordered pair is (2, 0).

Thus, we get the two ordered pairs (0, -2) and (2, 0).

Step 6:

Now, plot these two ordered pairs on the same coordinate plane and join them.

The resulting graph is as shown.

Step 7:

Now, identify the point of intersection of the two lines. Here in the graph the two lines are parallel to each other. Parallel lines never intersect each other.

Step 8:

So, there is no solution for the given system of equations and the given system of equations is inconsistent.

Solving system of equations with three variables:

We can also solve the system of equations in three variables by graphing. Systems of equations with three variables represent planes. Draw the graph of three equations in a three dimensional plane and look for the point of intersection. The point of intersection is the solution of the system of equations.

 Hold on. It is not so easy to draw planes in a piece of paper. You need a graphic calculator to do that. Moreover, in most of the cases it is really hard to find the point of intersection. It is not advisable to use graphing calculator to solve system of equations with three variables.
I suggest you to use substitution method or elimination method. The process of finding the solutions may be long but the solutions will be accurate.

Practice Questions:

Graph and solve the given linear equations

a) x-y = 4; x + 5y = -14

b) 3x + 5y = 2; 3x + 5y = -2

c) -9x + 8y = -2; 8x + 9y = 34

d) 3x + 4y = 8; 6x + 8y = 16

e) x - 2y = 2; 2x - 4y = 8

Related Articles:

>> Systems of Linear Equations: Consistent, Inconsistent, Dependent, Independent, Number of Solutions

You may also interested in this:

>> Differential and Integral Calculus: MCQ-1

>> Differential and Integral Calculus: MCQ-2

>> Venn diagram: Word problems

>> Equations in single variable: Quadrilaterals

>> Equations in single variable: Algebra

>> Age Word Problems