The solution of a quadratic equation in the standard form ax2 + bx + c = 0, where a, b, and c are real numbers and a ≠ 0, can be find using the quadratic formula given below.
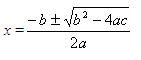
Let us work out a few examples.
Example 1:
Use quadratic formula to solve x2 - 2x - 35 = 0.
Solution:
Step 1:
Given equation is x2 - 2x - 35 = 0.
Here, a = 1, b = -2, and c = -35.
The quadratic formula is
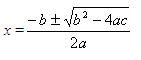
Step 2:
Substitute the values of a, b, and c in the quadratic formula to find the value of x.
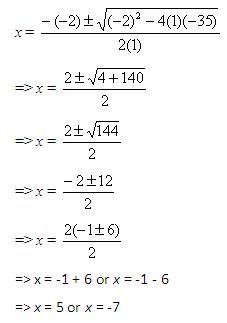
Step 3:
So, the solution set is {5, -7}.
Example 2:
Use quadratic formula to solve 4x2 + 2x = 17.
Solution:
Step 1:
Given equation is 4x2 + 2x = 17.
It can be written as 4x2 + 2x - 17 = 0. The equation is in the form of ax2 + bx + c = 0, where a = 4, b = 2, and c = -17.
Step 2:
The quadratic formula is
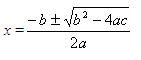
Substitute the values of a, b, and c in the quadratic formula to find the value of x.
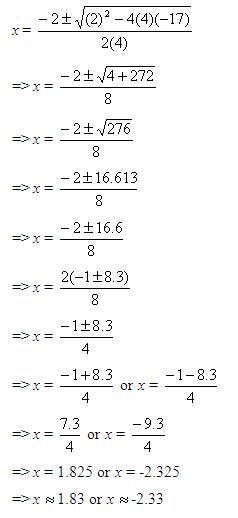
Step 3:
So, the solutions are 1.83 and -2.33.
Practice questions:
Solve the given quadratic equations using quadratic formula:
1. x2 – x – 12 = 0
2. 2x2 – 9x – 5 = 0
3. 6x2 + x – 48 = 0
4. x2 – 49 = 0
5. x2 + 3x – 18 = 0
Quadratic formula is a best method to solve any quadratic equations. Practice with more quadratic equations using quadratic formula to solve it.
Note: Calculator shows answer in decimals not in fraction.
Related Articles: