If the given quadratic equation is not a perfect square, then we need to make that as a perfect square. To make any quadratic expression as a perfect square, we need to use the method of completing the square as listed:-
1) Check for the following for the given quadratic equation, ax2 + bx + c = 0.
(a) If the given quadratic equation has the coefficient of x2 term as 1, then proceed to step (c).
(b) If the coefficient of x2 is not 1, then make it 1 by dividing both the sides of the equation by the coefficient.
(c) Isolate the x and x2 terms on one side and the constants on the other side of the equation.
2) Divide the co-efficient of x by 2 (That is b/2 ).
3) Find the square of b/2 (That is (b/2)2).
4) Add the resultant number (b/2)2 to both sides of the given equation and simplify it.
Let us solve a few quadratic equations by using completing the square method.
Example 1:
Solve x2 + 4x + 3 = 0 by completing the square.
Solution:
Step 1:
The given quadratic equation is x2 + 4x + 3 = 0. To solve by completing the square rewrite the given equation as a perfect square.
Here, the coefficient of x2 is 1.
So, isolate the x and x2 terms to one side and the constant to the other side by subtracting 3 from both sides of the quadratic equation.
x2 + 4x + 3 - 3 = 0 - 3
=> x2 + 4x = -3
Step 2:
Now, divide the coefficient of x by 2.
=> 4 ÷ 2 = 2
Step 3:
Find the square of 2.
i.e., 22 = 4
Step 4:
Now, add 4 on both the sides of the equation x2 + 4x = -3 and simplify.
x2 + 4x + 4 = -3 + 4
=> x2 + 4x + 4 = 1
Since, x2 + 4x + 4 = (x + 2)2, the equation becomes
(x + 2)2 = 1
Step 5:
Take square roots on both sides and simplify.
=> x + 2 = 1 or x + 2 = -1
=> x = 1 - 2 or x = -1 - 2
=> x = -1 or x = -3
So, the solutions are -1 and -3.
Step 6:
Check:
We can also check the solution by substituting it in the quadratic equation.
If x = -1, then
x2 + 4x + 3 = (-1)2 + 4(-1) + 3
= 1 - 4 + 3
= 4 - 4 = 0
This is true.
If x = -3, then
x2 + 4x + 3 = (-3)2 + 4(-3) + 3
= 9 - 12 + 3
= 12 - 12 = 0
This is true.
Step 7:
So, the solution set of the given quadratic equation is {-1, -3}.
Example 2:
A rectangular park is 10 m wide and 12 m in length. A pathway is constructed for pedestrians around the park. The area of the park including the pathway is 255 square meters. Find the width of the pathway.
Solution:
Step 1:
Length of the rectangular park = 12 m
Width of the rectangular park = 10 m
Let the width of the pedestrian path be x meters.
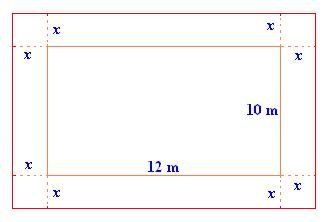
Step 2:
Area of the rectangular park = Length * Width
= 12 m × 10 m = 120 square meters
Step 3:
Length of the park after constructing the pedestrian path = 12 + x + x = 12 + 2x
New length = 12 + 2x meters
Width after constructing the pedestrian path = 10 + x + x = 10 + 2x
New width = 10 + 2x meters
Area of the park including the path = 255 square meters
New length * New width = 255 square meters
(12 + 2x)(10 + 2x) = 255
120 + 24x + 20x + 4x2 = 255
120 + 44x + 4x2 = 255
4x2 + 44x + 120 - 255 = 0
4x2 + 44x - 135 = 0
Step 4:
Now, solve this quadratic equation by completing the square. The coefficient of x2 is not 1. So, divide the equation by 4 on both the sides.
x2 + 11x – 135/4 = 0
Isolate the x and x2 terms.
Add 135/4 on both sides of the equation.
x2 + 11x - 135/4 + 135/4 = 0 + 135/4
=> x2 + 11x = 135/4
Step 5:
Now, the coefficient of x is 11. Divide it by 2 and square it. So, it becomes
(11/2)2 = 121/4
Step 6:
Now, add 121/4 on both sides of the equation x2 + 11x = 135/4.
x2 + 11x + 121/4= 135/4 + 121/4
=> x2 + 11x + 121/4= 256/4
=> x2 + 11x + 121/4= 64
In the equation, x2 + 11x + 121/4 is a perfect square. So, it the equation can be written as,
(x +11/2) 2 = 64
Take square roots of both the sides.
x + 11/2 = 8 or x - 11/2 = -8
=> x = 8 - 11/2 or x = -8 - 11/2
=> x = 5/2or x = -27/2
=> x = 2.5 or x = -13.5
We are looking for the width of the pathway and the width (distance) cannot be negative.
So, ignore the negative number.
=> x = 2.5
Step 7:
Related Articles: