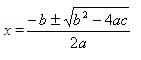In this method, we are going to find the solution or roots of a quadratic equation graphically. The graph of a quadratic equation is always a parabola. The points where the graph of the parabola cuts the x-axis are called the roots of the corresponding quadratic equation.
To graph a quadratic equation, we should graph the related quadratic function. For example, if the quadratic equation is x2 + 2x + 5 = 0, then the related quadratic function is f(x) = x2 + 2x + 5.
Let us solve few problems on quadratic equations by graphing.
Example 1:
Solve x2 + x - 6 = 0 by graphing.
Solution:
Step 1:
Given equation is x2 + x - 6 = 0.
Here a = 1, b = 1, and c = -6.
Graph the related function f(x) = x2 + x - 6.
The equation of the axis of symmetry is x = - b/2a
x = - b/2a = - 1/2(1) = - 1/2 = -0.5
=> x = -0.5 is the axis of symmetry of the equation.
Step 2:
When x = -0.5,
f(x) = f(-0.5) = (-0.5) 2 + (-0.5) - 6 = 0
=> f(-0.5) = 0.25 - 0.5 - 6 = -6.25
So, the coordinates of the vertex are (-0.5, -6.25).
Step 3:
Now, make the table with all other points.
Put x = -4, -3, -2, 0, 1, 2, 3 and find f(x).
When x = -4,
f(x) = f(-4) = (-4)2 + (-4) - 6 = 16 - 4 - 6 = 6
When x = -3,
f(x) = f(-3) = (-3)2 + (-3) - 6 = 9 - 3 - 6 = 0
When x = -2,
f(x) = f(-2) = (-2)2 + (-2) - 6 = 4 - 2 - 6 = -4
When x = -1,
f(x) = f(-1) = (-1)2 + (-1) - 6 = 1 - 1 - 6 = -6
When x = 0,
f(x) = f(0) = (0)2 + (0) - 6 = 0 + 0 - 6 = -6
When x = 1,
f(x) = f(1) = (1)2 + (1) - 6 = 1 + 1 - 6 = -4
When x = 2,
f(x) = f(2) = (2)2 + 2 - 6 = 4 + 2 - 6 = 0
When x = 3,
f(x) = f(3) = (3)2 + 3 - 6 = 9 + 3 - 6 = 6
x |
-4 |
-3 |
-2 |
-1 |
-0.5 |
0 |
1 |
2 |
3 |
f(x) |
6 |
0 |
-4 |
-6 |
-6.25 |
-6 |
-4 |
0 |
6 |
Hence, the ordered pairs of the quadratic function are (-4, 6), (-3, 0), (-2, -4), (-1, -6), (-0.5, -6.25), (0, -6), (1, -4), (2, 0), and (3, 6).
Step 4:
Now, plot the ordered pairs in a coordinate plane and join the points.
The point where the related function f(x) = 0 is the solution to this quadratic equation. This occurs at the x-intercepts. The x-intercepts are the points where the graph touches the x-axis. So, the graph has -3 and 2 as x-intercepts.
So, the solutions are -3 and 2.
Step 5:
Check:
We can also check our solutions by factoring the given equation.
x2 + x - 6 =0
=> x2 + 3x - 2x - 6 = 0
=> x(x + 3) - 2(x + 3) = 0
=> (x + 3)(x - 2) = 0
Using the zero product property,
x + 3 = 0 or x - 2 = 0
x = -3 or x = 2
Step 6:
So, the solutions of the equation are -3 and 2.
Example 2:
Solve x2 - 10x + 25 = 0 by graphing.
Solution:
Step 1:
Given equation is x2 - 10x + 25 = 0.
Here a = 1, b = -10, and c = 25.
Graph the related function f(x) = x2 - 10x + 25.
The equation of the axis of symmetry is x = - b/2a
x = - b/2a = - 10/2(1) = - b/2a = 5
=> x = 5 is the axis of symmetry of the given equation.
Step 2:
When x = 5,
f(x) = f(5) = (5)2 - 10(5) + 25 = 25 - 50 + 25 = 0
=> f(x) = 0
So, the coordinates of the vertex are (5, 0).
Step 3:
Now, make the table with all other points.
Put x = 2, 3, 4, 6, 7, 8 and find f(x).
When x = 2,
f(x) = f(2) = (2)2 - 10(2) + 25 = 4 - 20 + 25 = 9
When x = 3,
f(x) = f(3) = (3)2 - 10(3) + 25 = 9 - 30 + 25 = 4
When x = 4,
f(x) = f(4) = (4)2 - 10(4) + 25 = 16 - 40 + 25 = 1
When x = 6,
f(x) = f(6) = (6)2 - 10(6) + 25 = 36 - 60 + 25 = 1
When x = 7,
f(x) = f(7) = (7)2 - 10(7) + 25 = 49 - 70 + 25 = 4
When x = 8,
f(x) = f(8) = (8)2 - 10(8) + 25 = 64 - 80 + 25 = 9
x |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
f(x) |
9 |
4 |
1 |
0 |
1 |
4 |
9 |
So, the ordered pairs of the quadratic function are (2, 9), (3, 4), (4, 1), (5, 0), (6, 1), (7, 4), and (8, 9).
Step 4:
Now, plot the ordered pairs in a coordinate plane and join the points.
The resultant graph will be as shown.
The point where the related function f(x) = 0 is the solution to this quadratic equation. This occurs at the x-intercepts. The x-intercepts are the points where the graph touches the x-axis.
Notice that the vertex of the parabola is the x-intercept.
Hence, the solution is 5.
Step 5:
Check:
Let us check it by factoring.
Factor the equation x2 - 10x + 25 = 0.
x2 - 5x - 5x + 25 = 0
=> x(x - 5) - 5(x - 5) = 0
=> (x - 5)(x - 5) = 0
=> x - 5 = 0 or x - 5 = 0
=> x = 5 or x = 5
So, there are two roots but they are identical.
So, this quadratic equation has only one root called 5 as double root.
Step 6:
So, the solution is 5.
Example 3:
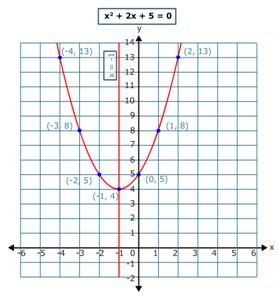
Solve x2 + 2x + 5 = 0 by graphing.
Solution:
Step 1:
Given equation is x2 + 2x + 5 = 0.
Here, a = 1, b = 2, and c = 5.
Graph the related function f(x) = x2 + 2x + 5.
The equation of the axis of symmetry is x = - b/2a
x = - b/2a= - 2/2(1) = -1
=> x = -1 is the axis of symmetry of the given equation.
Step 2:
When x = -1,
f(x) = f(-1) = (-1)2 + 2(-1) + 5 = 1 - 2 + 5 = 4
So, the coordinates of the vertex are (-1, 4).
Now, make the table with all other points.
Put x = -4, -3, -2, 0, 1, 2 and find f(x).
When x = -4,
f(x) = f(-4) = (-4)2 + 2(-4) + 5 = 16 - 8 + 5 = 13
=> f(-4) = 13
When x = -3,
f(x) = f(-3) = (-3)2 + 2(-3) + 5 = 9 - 6 + 5 = 8
=> f(-3) = 8
When x = -2,
f(x) = f(-2) = (-2)2 + 2(-2) + 5 = 4 - 4 +5 = 5
=> f(-2) = 5
When x = 0,
f(x) = f(0) = (0)2 + 2(0) + 5 = 5
=> f(0) = 5
When x = 1,
f(x) = f(1) = (1)2 + 2(1) + 5 = 1 + 2 + 5 = 8
=> f(1) = 8
When x = 2,
f(x) = f(2) = (2)2 + 2(2) + 5 = 13
=> f(2) = 13
x |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
f(x) |
13 |
8 |
5 |
4 |
5 |
8 |
13 |
So, the ordered pairs of the quadratic function are (-4, 13), (-3, 8), (-2, 5), (-1, 4), (0, 5), (1, 8), and (2, 13).
Step 3:
Now, plot the ordered pairs in a coordinate plane and join the points.
The resultant graph will be as shown.
The point where the related function f(x) = 0 is the solution to this quadratic equation. This occurs at the x-intercepts. The x-intercepts are the points where the graph touches the x-axis. So, the graph has no x-intercept.
Step 4:
So, there are no real number solutions for the given quadratic equation.
Related Articles: